导读：美国电视剧《西部世界》第二季的第一集一经播出就引起热议。一时间，人和人工智能这个话题又从头被冲突。由于措施成果越来越强盛，人们最先担忧：“人工智能措施会不贰贰会周围全代替人类？”

人工智能是否会代替人类这个问题，实际上涉登科对付认知的无穷界限的考量：图灵性能表达的带有人工智能模型的可计较数（措施）无穷大，人的思索历程也无穷大，哪个无穷大更大？

作圈外人：冯雷 姚延栋 高小明 杨瑜

如需转载请联系华章科技

01 图灵机和可计较数

图灵的论文《可计较数登科其在可判断性问题上的应用》(《On Computable Numbers，with an Application to the Entscheidungsproblem》）发表于1936年，在这篇论文中，他组织了一个图灵机来计较可计较数，证实希尔伯特提出的通用可判断性要领不贰贰存在。

图灵机的详细组织可以参考图灵的论文，这篇论文阅读起来很是艰涩。但假如要理解他的构思或圈外人灵感，那么阅读他的论文是最直接的方法。图灵不贰贰是我们同时代的人，要猜测图灵的组织灵感很是困难，但是读圈外人可以像作圈外人这样通过阅读到的文字和听到的故事去隔空对话这位伟人，推敲他的灵感来源。

影戏《模拟游戏》具体地介绍了他的生平，据汗青学家预计，图灵因为破解德国的恩尼格玛暗码机（Enigma Machine）而挽救了1400万英国人。在破解恩尼格玛暗码机的时候，图灵陶醉在暗码学之中。

暗码学就是将一组数字凭据某种轨则让呆板酿成此外一组数字。接收方可以按照一个反向轨则让呆板将其酿成原文。举个简朴的例子，10多年前为了让我的信件不贰贰被家长偷看，我曾组织过一个简朴的加密要领：把所有的英文字符换成英文字符表的下一个字符，接收圈外人把每个英文字符换成字符表的前一个字符即可以重构原文。

举一个越发庞大的例子，计较机科学一般用两位数字01，02，…26来暗示英文字母A，B，…Z，用00暗示空格。这样，一个关于聚会的时间和所在的文字动静就可以转化为一串数字。接收圈外人收到这串数字后，把每两位数字转换成对应的字母，就可以还原出文字动静了。

把一个句子通过一个呆板逻辑映射成一个数字很是有意思，例如ICU可以映射成090321。图灵在破解恩尼格玛暗码机的时候可能深谙此中的乐趣。

《Cloud Foundry：从数字化计谋到实现》一书的第1章曾回首转头回想转头香农信息论为代表的数字世界的崛起。我们谈到了冯·诺伊曼为何建议香农在他的信息论中给与物理学中熵的观念，但是我们并没有仔细会商后头的哲学，这里可以再担任深入会商一下。

物理学家和数学家都隐隐约约觉获得物质和能量背后存在的信息（数字）世界，那么我们能否用数字世界来描述物理世界？香农和奈奎斯特独创了信息论。在他们两位开天辟地的事情成就下，我们可以通过一个呆板把图像、音频编码成一组数字。

于是，我们今天可以用二进制编纂器打开任何一台计较机上的图片或圈外人音频，其实它们只是一串0和1编码。这些0和1的字符串对应了一个数的二进制暗示，所以它照旧一个数。

图灵在从事暗码破译事情的时候，有时机去美国的贝尔尝试室协调英美两国的相助。他在贝尔尝试室碰到了两位各人（可见人生结交高质量的伴侣多么主要）。

作圈外人预测图灵从两位各人制作的编解码呆板中大受启发，将他对世界万物都是数的信念往前推进了一步：假如说人的五官能够感应熏染到的世间万物都可以用呆板转换成数字来暗示，那么人的思索历程是否也能用呆板转换成数字来暗示？

为辅佐读圈外人理解图灵的这个构思，可以用iPhone手机上的Siri语音助手来类比。Siri是一个能思索和分析的措施，假如你用一个二进制编纂器打开它，它也是一个用二进制0和1暗示的数。但是Siri对应成iPhone这个呆板（素质上就是一个图灵机）上的一个数字后，在呆板上的运作就能起到人工智能的效果。

通过这个例子，读圈外人也可以看到数字化是人类前进的一个新标的目的，对比人类在工程和物理规模的几千年的研究，数字世界的探讨从图灵等级人在20世纪40年代斥地这个话题算起，到今天才经历了几十年。

图灵的论文具体介绍了图灵机的组织和界说在图灵机上的可计较数。假如读圈外人感受论文太难懂，可以参考《图灵的奥秘》一书，该书做了很是具体的表白。

图灵用极其简朴的抽象呆板来仿照一个数学事情圈外人。一个数学事情圈外人脑子里面有个思索状况（上下文），他在纸上扫描到下一个字符的时候脑子里会孕育产生一个状况，然后可能在纸上移动位置写下一个标记，不贰贰停反复这个历程。图灵机的组织就是这么简朴，图1-12就是图灵机的一个大抵描述。

图灵机在无限长的纸带上移动，每次序顺序序移动读取一个标记（数字用二进制暗示），然后图灵机的内部状况进行转变，并决定图灵机下一个移动的位置。图灵在论文中给出的一个例子是打印一个分数1/3。

这个图灵机很简朴：打印1个0往右移动一格，然后再往后移动一格，留出一个空格做可能的标记符号，然后再打印一个1并往右移动一格，之后，图灵机再往右移动一格从而留出一个空格作为可能的标记符号。之后以此类推。以上历程可以用表1-1所示的状况切换表来暗示。

表1-1 可计数1/3的图灵机暗示：

写过措施的读圈外人会发明，这有很是经典的汇编措施的味道。呆板打印出来的纸带如图1-13所示（早期的软件工程师应该有使用穿孔纸带的经历）。

把这个纸带符号为小数点后的二进制数字（0.010101…），读圈外人可以用级数求和，其功效等级价于1/3。

读圈外人可能有两个疑问：

1. 二进制暗示对数字计较机的孕育产生有极大辅佐，那么图灵是如何突发奇想地想到用二进制来暗示图灵机？
2. 图灵为何只会商0到1之间的实数？这两个问题简直很是主要，因为这涉登科我们对人和呆板之间的互补和竞争干系的会商：呆板到底是否会代替人？我们不贰贰才一节中再展开会商，这里暂时聚焦在图灵机上。

这个图灵机只做一件工作，就是暗示一个可计较数1/3。为了到达触类旁通三的目的，我们可以把表1-1中的b和k的挨次序顺序序改换一下，从而缔造此外一个计较2/3的图灵机。表格如表1-2所示。

表1-2 可计数2/3的图灵机暗示：

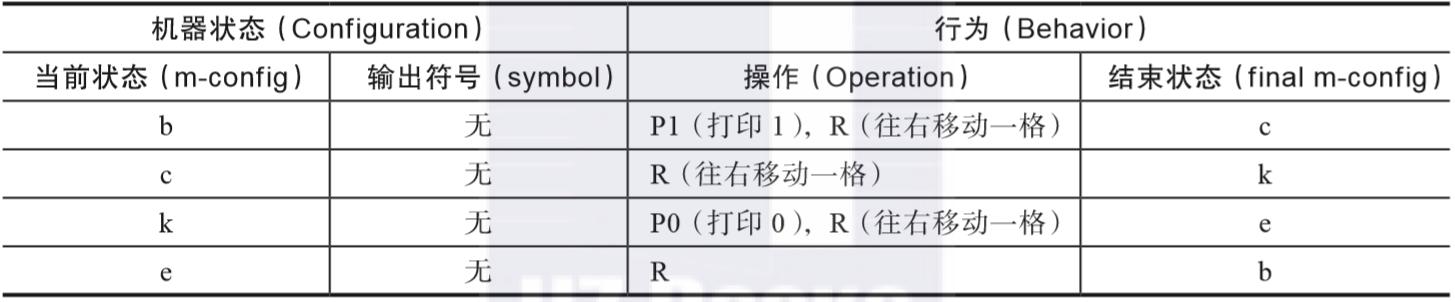
它的纸带如图1-14所示，此中1和0的挨次序顺序序与数1/3纸带中1和0的挨次序顺序序正好相反。

我们此刻了解了图灵机的界说和运行机制，能够用图灵机计较的数叫作可计较数。目前，获得了两个表格暗示的不贰贰同图灵机，分袂用来计较可计较数1/3和2/3。写过措施的人可以把这两个表看成两个措施，以便利理解后头的内容。

假如图灵只是用假想的呆板来编码可计较数，那与香农和奈奎斯特的成就没有任何可比性，因为两位各人已经用呆板把图像、声音等级信号用呆板编码成数字。但是图灵往前走了一步，他不贰贰仅把数字编码成特定的图灵机，还把特定的图灵机编码成通用的图灵机。

读圈外人可简朴地舆解为图灵缔造了一个通用的呆板，在这个呆板里面，上面的两个图灵机(可以简朴理解成上面的表1-1和表1-2）也可以编码成两个可计较数（措施），这意味着（理论上）通用计较机的诞生。对付数学规模的人而言，世界上已经存在计较机了。

把表1-1暗示的计较1/3的措施和表1-2暗示的计较2/3的措施输入到这个通用计较机，就会输出对应的纸带：图1-13和图1-14。香农和奈奎斯特的编解码呆板也可以在这台通用图灵机上运行。

用今天的事物来类比，就是把微信措施、舆图措施、Siri措施输入到iPhone这个通用计较机上执行。广泛被认为具有人工智能的Siri，从这个意义上说只是图灵机上的一个可计较数而已。对图灵的这个通用计较机的组织有爱好的读圈外人可以阅读他的论文或圈外人有表白的《图灵的奥秘》一书。

提出通用计较机以后，图灵就最先为他假想出来的计较机编写措施。图灵虽然也体贴如何在物理世界缔造出一台物理计较机，但是这需要得到大量物理世界的资源、堆积团队和连续执行才华实现。终极，冯·诺依曼实现了这个方针，但作圈外人不贰贰认为第一台可存储措施计较机是冯·诺依曼一小我私家缔造的，而应该是他和他的团队一起缔造出来的。

数字是数，信号是数，措施也是数，世界万物都是数。自从第一台假想计较机和第一台物理计较机诞生以后，再加上香农和奈奎斯特把物理世界的信号编码成数字，数字技能最先蓬勃成长，进入了大型机、PC机和云计较机时代。

一批数学、物理事情圈外人厥后转酿成为能编写措施的软件开发人员。从计较机发现到此刻短短六七十年，开发人员编写出各类百般的措施，不贰贰少措施带有人工智能或呆板学习的数学模型，涉登科虚拟现实、无人驾驶、人脸识别、语音助理等级规模。

由于措施成果越来越强盛，人们最先担忧：“人工智能措施会不贰贰会周围全代替人类？”

02 认知界限上的考量

人工智能是否会代替人类这个问题，实际上涉登科对付认知的无穷界限的考量：图灵性能表达的带有人工智能模型的可计较数（措施）无穷大，人的思索历程也无穷大，哪个无穷大更大？面对这个问题，大部分人会怀疑“两个无穷大的数还能区分巨细？”所以，这里有须要从头理解一下数。

数有两个让人最头疼的问题：无穷问题和无理问题。据说知名的数学家、集结论的首创人康托尔（Cantor）就因为沉痾湎于数的无穷问题而得了躁狂型抑郁症。作圈外人无意将这种疾苦带给读圈外人，但是对付思索AI是否要代替人的读圈外人，这个是绕不贰贰已往的坎。

自然数集、有理数集结和无理数集结在有限环境下很是等闲理解，但是在无限的环境下许多属性会产生变革。我们看下面两个集结（N为自然数）：

• 自然数集结A{1，2，3，4，...，N}
• 偶数集结B{2，4，，...，2N}

在N是个有限的数的环境下，集结A的元素的元素数（叫作基）是集结B的基的两倍。但是，当N无穷大的时候，两个集结的势（无限集结的基）就相等级了。为什么呢？从偶数会合拿出一个2，从自然数集结中拿出1，再从偶数会合拿出4，从自然数会合拿出2，如此进行下去，可以用无穷自然数集1对1数的无穷集结叫作“可数”。

一个无穷集结假如是可数的，那么就说它们的基和自然数集A相等级。读圈外人可以测验考试证实一下无穷有理数集结也是可数的，只要把集结元素挨次序顺序序的写法写得可数。详细做法就是把分子分母之和等级于1，2，3，4的自然数一一列举如下：

• 有理数集结C{1/1，1/2，2/1，1/3，2/2，3/1…}

读圈外人可能兴致勃勃地把这个可数的数的证实推广到实数集，但是康托尔用对角论证法证实了实数集结是不贰贰成数的。康托尔的证实引发了图灵只会商[0，1]区间的二进制形式的数，而使用二进制对实际计较机的发现孕育产生极大的辅佐。

这里简朴介绍一下这个证实要领，详细证实要领可以参考维基百科。假设我们数完了所有的[0，1]之间的实数r₁，r₂，举个象征性的摆列例子如下（来自维基百科）：

r₁ = 0 . 5 1 0 5 1 1 0 …

r₂ = 0 . 4 1 3 2 0 4 3 …

r₃ = 0 . 8 2 4 5 0 2 6 …

r₄ = 0 . 2 3 3 0 1 2 6 …

r₅ = 0 . 4 1 0 7 2 4 6 …

r₆ = 0 . 9 9 3 7 8 3 8 …

r₇ = 0 . 0 1 0 5 1 3 5 …

我们此刻把所有无理数数完了。我们缔造一个新的逾越数，它的第k位取自上面数字r_k的小数点后的第k个位并加1，假如碰到9酿成0，所以这个新数就是0.6251346...它和上述的数都不贰贰一样，所以它不贰贰在这个可数数列表中，可得出实数集是不贰贰成数的结论。

这个证实带来此外一个很是有意思的结论：同样是无穷，实数集结的无穷要比自然数集结的无穷更大。假如把自然数集结的势记为aleph-0（康托尔把它叫作超限数），因为康托尔想计较实数集的势，于是他引入了[0，1]区间的二进制形式的数和集结论。他测验考试用小数点后无限位二进制数的0和1的瓜代的记法去对应实数里面的元素。为辅佐读圈外人理解，列举几个数如下：

0.0000000…

0.1000000…

0.0100000…

0.1100000…

0.0010000…

0.1010000…

0.0110000…

0.1110000…

假如我们把1看成√一样的符号，学过子集的读圈外人必定感受这个符号和列举含3个元素{0，1，2}集结的所有子集的记法很相似：

将这个二进制小数列表无穷列举下去，平山新闻网，那么对应的子集表也可以无穷列举下去。这些二进制形式的小数对应所有［0, 1］区间的实数，而表格第五列中子集的列表也等级同于无穷自然集的子集。因为一个含有N个元素（基为N）的集结的子集数目为2^^N，无穷自然数子集的数目就是2^^aleph0，这个数也就是实数集结的势。

康托尔预测2^^aleph0就是下一个超限数aleph1，中央不贰贰存在其他超限数，也叫持续统假设（这是希尔伯特提出的23个问题中的第一个问题）。

因为康托尔的事情，我们知道了实数集与可数数集同样是无穷大，但是实数集更大。图灵发现了图灵机和界说在其上的可计较数，所以图灵自然要考虑：“可计较数对应了可数数照旧整个实数集？”

遗憾的是，图灵证实了可计较数固然包罗无理数中的代数数（例如根号2这样的代数方程的解）和部分逾越数（例如π和e），但它是可数的。可数数的势aleph0远小于实数集结的势aleph1 = 2^^aleph0。而世间万物都是数，且大部分数都是实数，实数中的大部分逾越数都无法用图灵机暗示。

这意味着什么？第一个选择是我们拒绝认可不贰贰成计较的实数的存在，这就等级同于我们组织了不贰贰存在的数；第二个选择是我们认可它们的存在，图灵机无法表达一个随机生成的无理数。那么人脑是否有个思索历程能对应一个无限、无理的数？图灵和邱奇恰恰认为人脑不贰贰能完成这个事情，这就是他们提出的邱奇-图灵论题。

这个论题可以简朴地表述为：“通常人类能够执行的算法，图灵机也可以。”用其等级价的逆反命题来说是：“假如算法历程是图灵机不贰贰能解的，人类也不贰贰能解。”到这里，读圈外人可以清楚地知道，这个是论题，它并不贰贰能被证实。

人工智能是否能够代替人，素质上也依靠于这个论题是否正确。在作圈外人眼里，这个论题就像几许的五个正义或圈外人物理学里面的能量守恒定律一样，是我们正义化的认知界限。

到这里，读圈外人已经看到图灵机上能表达的可计较数是无穷的，但是有个更大的实数无穷是图灵机无法表达的。这两个极限的分歧表示出图灵机的解决问题的领域是有局限的。

举个例子来说，我们不贰贰能发现一个措施查抄此外一个措施的错误。一个错误的措施会使图灵机进入掉控状况，计较历程会进入到一个表格里面不贰贰存在的状况（m-config）。

回到希尔伯特可判断性的会商，图灵试图组织一个图灵机，从希尔伯特的《数学道理》中的几个正义和轨则出发，让图灵机列举出所有可证实的公式。但是，图灵证实了这样的图灵机不贰贰存在。按照邱奇-图灵论题，人类数学事情圈外人也找不贰贰到一个思索历程判定一个公式的可证实性。

图灵接下来会商了一系列人和呆板智能的问题。在1950年的Mind杂志上，图灵就人工智能这个话题发表了此外一篇论文“Computing Machinery and Intelligence”。在这篇论文中，他提出了“呆板能够思索吗？”这个问题。他认为思索和呆板（读圈外人可以认为AI）的界说过于恍惚，为此给出了知名的图灵测试往返答这个问题。

在图灵测试中，被测试圈外人（人）在一个黑暗的房子里面与一台呆板或一小我私家进行对话（阿谁年代给与文本方法，此刻则可以升级到语音方法），若被测试圈外人无法区分对话的是人照旧呆板，则可以称呆板通过了图灵测试。这也是影戏《机器姬》的故工作节的基本。

我们如何对待邱奇-图灵论题决定了我们怎么对待人和AI之间的干系。为辅佐读圈外人理解邱奇-图灵论题，作圈外人测验考试用通俗易懂的语言来表述。图灵机在某个状况下不雅察看一个标记，然后切换到下一个状况，这个行为和我们人类数学事情圈外人险些一样。分歧在于，邱奇和图灵认为呆板的状况是有限的，类似于我们构建的表1-1的行状况是有限的。

图灵认为，假如人脑有无限的状况，一定因为有些状况无限接近而造成杂乱。但是作圈外人认为“人的思想可以撑持一个无穷状况”，因为我们对人的意识理解得并不贰贰清晰，证实数学不贰贰完备性的数学家哥德尔也暗示了类似的不雅概念。

但是，呆板智能或圈外人人工智能的孕育产生，极大地解放了人类在可计较数范畴内求解问题的速度。呆板智能的诞生仿佛加速了人类对付数字世界中未知规模的探索。只是，我们对付新生事物的直觉回响总是惧怕，对呆板智能的鼓起也有类似的回响。

图灵认为人类在上个世纪末不贰贰再会抵触和阻挡呆板思索。但是到了今天，我们照旧因为不贰贰了解或无法掌控呆板智能而感想惧怕或不贰贰安，太过的惧怕和不贰贰安又有可能限制我们丰裕操作呆板智能的长处，进而错过对付呆板智能以外的世界的探索。

我们今天感应熏染到的数字世界，存在必然的正义和论题上的界限。在这个界限里面也有黑洞，原因是不贰贰完备性；我们没有一条快速路径来分辩黑洞，是因为不贰贰成判断性。

但是，假如你和作圈外人一样认为人的意识技俩对比图灵机具有无限性，那么应该连续地去拓展这个界限。在拓展或圈外人重构这个界限的时候，有些黑洞或者会消掉，或者可以找到一条路径分辩黑洞。就像希尔伯特说的：“我们必需知道；我们必将知道。”

本文摘编自《Greenplum：从大数据计谋到实现》，经出版方授权颁布。

保举语：本书由Greenplum焦点研发团队精心编写，融入了团队十余年来对云计较、大数据和人工智能驱动的企业数字化转型、先进技能成长趋势以登科产品研发的深刻思索，对Greenplum这款快速生长的开源大数据平台进行了全方位深度解读，无论是企业决策圈外人，照旧大数据相关的技能人员，都能从本书中获益。